2018 X-NUCA 线上赛

发表于 更新于 分类于 ，

比赛日期：2018.11.24

在i春秋平台举办的X-NUCA线上赛，前20可以进线下赛。Aurora最终成绩为18名。

一共有三道re，我比赛时只做出了第一道，比赛结束后出了第二道。因为一直死磕第二题磕了太久所以根本没看第三道，第三道pizza做了，听说挺简单的，有时间再补上（咕咕咕）= =

题目，脚本及ida数据库下载：下载地址

_backup文件夹内为题目原题，其余的题目文件能被我打过补丁。

Code

进入main函数，接受了三个数字输入，sub_400806是vm的计算部分。bytecode在code文件里。指令和算法都很简单，都是对三个输入的加减乘除和位运算，用z3写脚本跑一下就行了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from z3 import *
x=BitVec('x',32)
y=BitVec('y',32)
z=BitVec('z',32)
s=Solver()
s.add(x&0xff==0x5E)
s.add(z&0xff==0x5E)
s.add(y&0x00ff0000==0x5E0000)
s.add((x>>4)*0x15-z==0x1D7ECC6B)
s.add((x>>8)+y==0x5FBCBDBD)
s.add((z>>8)*0x03+y==0x6079797C)
print(s.check())
m=s.model()
X=m[x].as_long()
Z=m[z].as_long()
Y=m[y].as_long()
print('X-NUCA{%x%x%x}'%(X,Y,Z))

Neural Network

神经网络，一个完全没接触过的全新领域。先查一波资料：

TensorFlow中文社区

tensorboard使用

Tensorflow 模型文件的使用以及格式转换

tensorflow只能在python3.5和python3.6安装，踩坑就踩了好久。

搭好环境直接跑一下它的python脚本，除了有个提示外都正常，提示可以在脚本开头加段代码去掉

1
2
import os 
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

运行一下python脚本，随便输点东西进去，然后弹出错误警告。似乎是大小不对，应该32个而不是16个。看一下脚本的内容，get_input函数里把输入rjust了16，改成32，这样就可以跑了，输出了Sorry, srcret wrong! Try harder?

分析一下脚本，结合各种地方找的资料，发现他读取了一个model.meta文件作为图，x应该是输入tensor，y是输出tensor。把输入放进黑盒操作一波得到输出，然后跟常量final比较，要求误差在1e-8之内。

看样子重点就在于它的model.meta这个文件里了。用hexeditor打开，只能看到一些字符串和数据。

在查一波资料，发现了tensorboard这个东西，他能把meta文件的内容转化成图，于是根据教程，得到了这个模型的模型图。

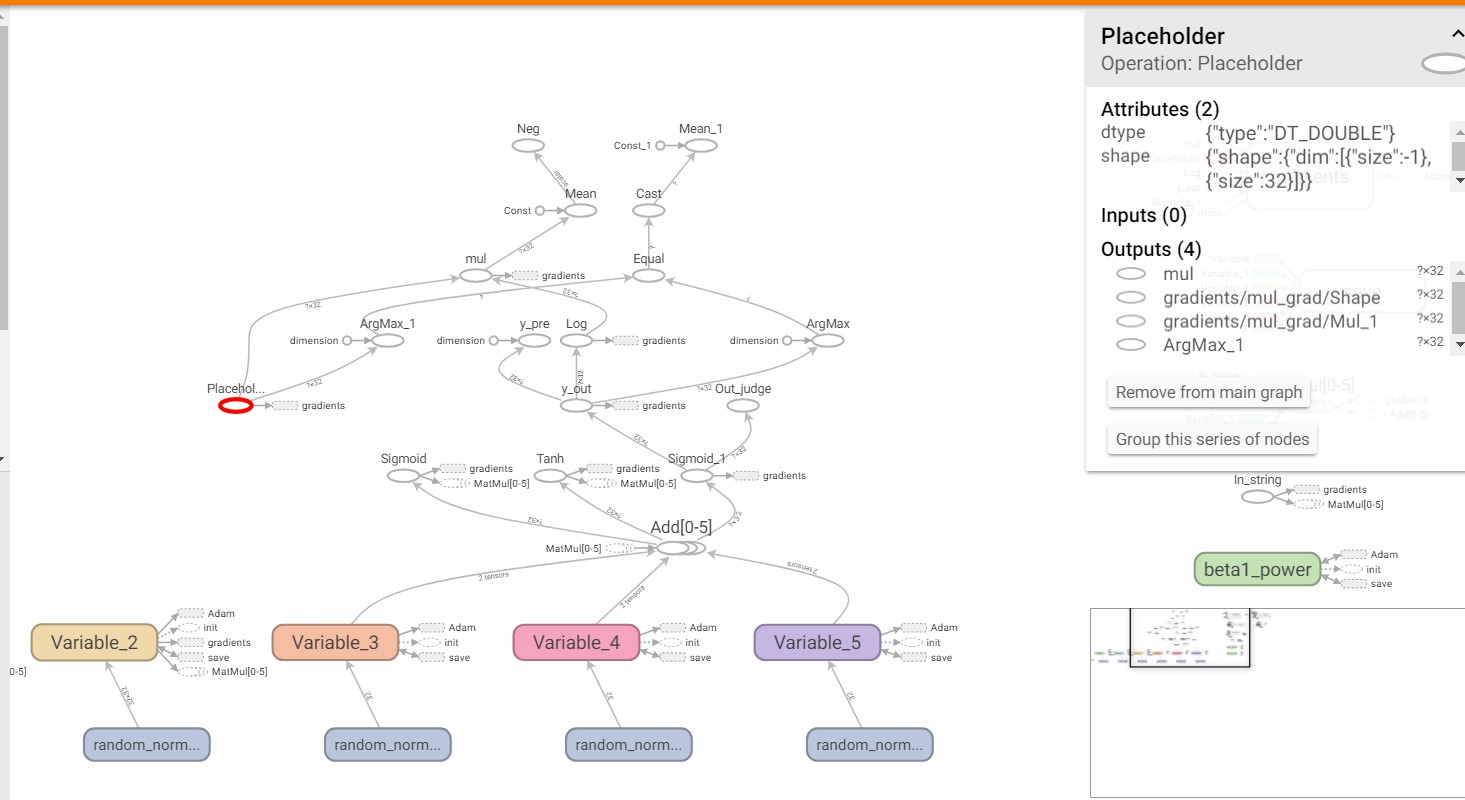2018xnuca1.jpg

点进各个节点可以看到每个节点的输入(Inputs)，输出(Outputs)和操作(Operation)。于是我们找到了In_string和Out_judge。跟着Out_judge的操作沿着输入一步一步往前走，能找到In_string。这些个过程就是黑盒的过程了。注意其中有很多的分支是没用到的，不必理会。最终整理出正向的操作（用tensorflow的函数表示）：

1
2
3
4
5
6
7
8
9
t0 = tf.matmul(In_string, v0)
t1 = tf.add(t0, v3)
t2 = tf.sigmoid(t1)
t3 = tf.matmul(t2, v1)
t4 = tf.add(t3, v4)
t5 = tf.tanh(t4)
t6 = tf.matmul(t5, v2)
t7 = tf.add(t6, v5)
t8 = tf.sigmoid(t7)

matmul：矩阵相乘

sigmoid：S型生长曲线，具体可以百度

add:两个矩阵对应量相加

tanh：双曲正切

relu：正数不变，负数变为为0

这里的v0到v5都是常量。参考脚本中res的用法，可以拿到数据：

1
2
3
4
5
6
7
8
9
10
def gn(nm):
    return sess.run(nm + ":0", feed_dict={x:[X]})

In_string = gn("In_string")
v0 = gn("Variable/read")
v1 = gn("Variable_1/read")
v2 = gn("Variable_2/read")
v3 = gn("Variable_3/read")
v4 = gn("Variable_4/read")
v5 = gn("Variable_5/read")

为了方便调试，我们定义：

1
2
3
def gv(v):
    return sess.run(v, feed_dict={x:[X]})
print(gv(a0))

直接print(t1)并不能输出它的值。参考之前的res，要把数据喂进去run一下，会返回一个numpy的array数据类型，于是这样就可以输出了。

同时，输出np.array时默认会省略一些数据用省略号代替，且输出的精度不足。为了更直观的观看，可以添加如下代码：

1
2
np.set_printoptions(threshold='nan')
np.set_printoptions(precision=20)

有了正向的输入过程，每个函数都是有反函数的，我们似乎就可以逆向得到输入了，逆向过程如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
from scipy.special import logit

def invsigmoid(a):
    b= np.array([[0.0]*32])
    for i in range(32):
        b[0][i]=logit(a[0][i]) #logit为sigmoid的反函数，但是tensorflow中没有这个函数，只能借助scipy中的了 
    return b

a = np.array([[1.40895243e-01, 9.98096014e-01, 1.13422030e-02, 6.57041353e-01,
    9.97613889e-01, 9.98909625e-01, 9.92840464e-01, 9.90108787e-01,
    1.43269835e-03, 9.89027450e-01, 7.22652880e-01, 9.63670217e-01,
    6.89424259e-01, 1.76012035e-02, 9.30893743e-01, 8.61464445e-03,
    4.35839722e-01, 8.38741174e-04, 6.38429400e-02, 9.90384032e-01,
    1.09806946e-03, 1.76375112e-03, 9.37186997e-01, 8.32329340e-01,
    9.83474966e-01, 8.79308946e-01, 6.59324698e-03, 7.85916088e-05,
    2.94269115e-05, 1.97006621e-03, 9.99416387e-01, 9.99997202e-01]])
a0=invsigmoid(a)
a1=tf.subtract(a0,v5)
a2=tf.matmul(a1,tf.matrix_inverse(v2))
a3=tf.atanh(a2)
a4=tf.subtract(a3,v4)
a5=tf.matmul(a4,tf.matrix_inverse(v1))
a6=invsigmoid(gv(a5))#a5是个tensor对象，要用np.array数据类型才能使用。
a7=tf.subtract(a6,v3)
a8=tf.matmul(a7,tf.matrix_inverse(v0))
l=gv(a8).tolist()
ll=l[0]
flag=''
for i in range(len(ll)):
    ll[i]*=128
    ll[i]=round(ll[i])
    flag+=chr(ll[i])
print(flag)

然而出问题了。最终的a8全是naf。让我们想办法输出中间变量的值，看看哪里有问题。在每一步后面输出a的数据。调着调着发现，第二个invsigmoid出了问题，意义不明（似乎是超出定义域了）。

思考了一下，我先随便输一个数据进去，用它算的结果逆一遍，看看能不能得到原来的值，于是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def trans(secret):
    return np.array([float(ord(x))/128 for x in secret])
fakeflag = "flag{01234567012345670123456789}"
X = trans(fakeflag)
sess = tf.Session()
saver = tf.train.import_meta_graph('model.meta')
saver.restore(sess, tf.train.latest_checkpoint('./'))
graph = tf.get_default_graph()
x = graph.get_tensor_by_name('In_string:0')
y = graph.get_tensor_by_name("Out_judge:0")
res = sess.run(y, feed_dict={x:[X]})

a0=invsigmoid(res)
a1=tf.subtract(a0,v5)
a2=tf.matmul(a1,tf.matrix_inverse(v2))
a3=tf.atanh(a2)
a4=tf.subtract(a3,v4)
a5=tf.matmul(a4,tf.matrix_inverse(v1))
a6=invsigmoid(gv(a5))#a5是个tensor对象，要用np.array数据类型才能使用。
a7=tf.subtract(a6,v3)
a8=tf.matmul(a7,tf.matrix_inverse(v0))
l=gv(a8).tolist()
ll=l[0]
flag=''
for i in range(len(ll)):
    ll[i]*=128
    ll[i]=round(ll[i])
    flag+=chr(ll[i])
print(flag)

到这里可以算回我的假flag，说明算法是没问题的。思前想后觉得应该是精度的问题。注意到体重final的精度是9位有效数字。我尝试把假flag得到的最终结果保留9位有效数字，再带进逆向算法中，就算不出假flag了。同时我逐步提高精度，发现要有14位以上有效数字的精度才能算出正确的输入！这让我不禁怀疑题目的正确性。找主办方交涉无果，只好重新找方向。

显然我们没办法提高数据的精度，一时间陷入了僵局。

查找资料解读meta的时候，除了用tensorboard看图形外，还发现了可以吧meta转成txt输出：

1
2
3
4
5
sess = tf.Session()
saver = tf.train.import_meta_graph('model.meta')
saver.restore(sess, tf.train.latest_checkpoint('./'))
graph = tf.get_default_graph()
tf.train.write_graph(graph, './aaa', 'train.pbtxt')

打开train.pbtxt，在这里可以看到所有的node，包括之前的Variable等。比赛时并没有太注意，只当用到的东西已经输出了。

最早看这个pbtxt的时候并没有很仔细，更多的跑去看tensorboard了。赛后重新看一下pbtxt，发现了很可疑的一段：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
node {
  name: "PRECISEFINAL"
  op: "Const"
  attr {
    key: "dtype"
    value {
      type: DT_DOUBLE
    }
  }
  attr {
    key: "value"
    value {
      tensor {
        dtype: DT_DOUBLE
        tensor_shape {
          dim {
            size: 1
          }
          dim {
            size: 32
          }
        }
        tensor_content: "!\3337\366\332\010\302?\3068c\rg\360\357?\002\\\336\266\224:\207?\367s\226\226{\006\345?\211\224C\366s\354\357?tkYQ\021\367\357?\303CE]Y\305\357?\207\005\215\237\370\256\357?\030\344\262\",yW?3\207\325\344\034\246\357?\267\335\336\356\370\037\347?\367\345j\354b\326\356?|\034lv\303\017\346?\210\242s\306\014\006\222?\372\353\304\254\341\311\355?\245\\\214\001\216\244\201?%\254@J\314\344\333?\030?\251\364\336{K?k\024R\313\002X\260?\331\361R\3329\261\357?\027U\364\033\243\375Q?#\031dW\265\345\\?\265b\315\225o\375\355?\022\207\375#q\242\352?H\330\273}\240x\357?A\362\214\203L#\354?L\000\207B\205\001{?\323\344\003\2171\232\024?\003\222)\3659\333\376>\372\241\322=\207#`?\361\324\024\0238\373\357?\037\013\327!\372\377\357?"
      }
    }
  }
}

这个名为PRECISEFINAL的node根本没见过，里面还藏有大量数据，难道这就是精确的final值？（名字都告诉你了是精确final了好吧）

把它带进脚本跑一下，flag就出了，而且直接查看它的数据可以发现它的精度是15位有效数字。

脚本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
import os 
import numpy as np
import tensorflow as tf
from math import isclose
from scipy.special import logit

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
np.set_printoptions(precision=20)
np.set_printoptions(threshold='nan')


def trans(secret):
    return np.array([float(ord(x))/128 for x in secret])

def gn(nm):
    a=graph.get_tensor_by_name(nm + ":0")
    return sess.run(a, feed_dict={x:[X]})

def gv(v):
    return sess.run(v, feed_dict={x:[X]})

def invsigmoid(a):
    b= np.array([[0.0]*32])
    for i in range(32):
        b[0][i]=logit(a[0][i])
    return b


fakeflag = "flag{01234567012345670123456789}"
X = trans(fakeflag)
#print(X)
sess = tf.Session()
saver = tf.train.import_meta_graph('model.meta')
saver.restore(sess, tf.train.latest_checkpoint('./'))
graph = tf.get_default_graph()
x = graph.get_tensor_by_name('In_string:0')
y = graph.get_tensor_by_name("Out_judge:0")
final = np.array([[1.40895243e-01, 9.98096014e-01, 1.13422030e-02, 6.57041353e-01,
    9.97613889e-01, 9.98909625e-01, 9.92840464e-01, 9.90108787e-01,
    1.43269835e-03, 9.89027450e-01, 7.22652880e-01, 9.63670217e-01,
    6.89424259e-01, 1.76012035e-02, 9.30893743e-01, 8.61464445e-03,
    4.35839722e-01, 8.38741174e-04, 6.38429400e-02, 9.90384032e-01,
    1.09806946e-03, 1.76375112e-03, 9.37186997e-01, 8.32329340e-01,
    9.83474966e-01, 8.79308946e-01, 6.59324698e-03, 7.85916088e-05,
    2.94269115e-05, 1.97006621e-03, 9.99416387e-01, 9.99997202e-01]])
res = sess.run(y, feed_dict={x:[X]})

In_string = gn("In_string")
v0 = gn("Variable/read")
v1 = gn("Variable_1/read")
v2 = gn("Variable_2/read")
v3 = gn("Variable_3/read")
v4 = gn("Variable_4/read")
v5 = gn("Variable_5/read")
precisefinal=gn("PRECISEFINAL")

a0=invsigmoid(precisefinal)
a1=tf.subtract(a0,v5)
a2=tf.matmul(a1,tf.matrix_inverse(v2))
a3=tf.atanh(a2)
a4=tf.subtract(a3,v4)
a5=tf.matmul(a4,tf.matrix_inverse(v1))
a6=invsigmoid(gv(a5))
a7=tf.subtract(a6,v3)
a8=tf.matmul(a7,tf.matrix_inverse(v0))
l=gv(a8).tolist()
ll=l[0]
flag=''
for i in range(len(ll)):
    ll[i]*=128
    ll[i]=round(ll[i])
    flag+=chr(ll[i])
print(flag)

Strange Interpreter

pizza:

程序里有012345abcdefghijklmnopqrstuvwxyz 直接输入进去 然后输出校验结果的时候看0x6130D0 直接就有前半部分 替换了前半部分 再带后半部分 后半部分也有了